Aby wyeliminować te problemy maszyna powinna w miarę możliwości utrzymywać prędkość posuwu na poziomie zadanym przez operatora. Maksymalna prędkość w węźle pomiędzy wektorami powinna być uzależniona od konta pomiędzy nimi i kształtu ścieżki narzędzia którą wektory te reprezentuje (rys. 5.4). Rozwiązaniem może być analizowanie więcej niż jednego wektora na raz, co umożliwi uzyskanie niezerowej wartości prędkości w węzłach ścieżki narzędzia. Niestety nie możemy analizować tylko jednego wektora w przód, ponieważ może być on (one) na tyle krótki, że nie będzie możliwe na jego długości zmniejszenie prędkości do wartości jej ograniczenia na końcu danego wektora. Konieczna jest więc analiza iteracyjna kolejnych wektorów i takie modyfikowanie (podbijanie) początkowo zerowych prędkości w węzłach pomiędzy wektorami, które spełni zakładane ograniczenia co do prędkości w węzłach ścieżki narzędzia, a jednocześnie ograniczy czas w którym narzędzie porusza się z prędkością mniejszą niż zadaną.
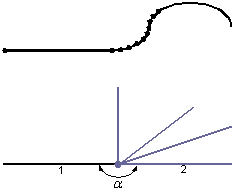
Dynamiczna analiza wektorów. Dla α = 0 Vp = Vmax; α > 90˚ Vp = 0; 90˚ > α > 0 prędkość przejścia Vp w węźle jest nieliniowa funkcją kąta α , uzależnioną od charakterystyki napędów i kształtu ścieżki narzędzia (α - kąt zawarty pomiędzy kolejnymi wektorami, Vp – prędkość przejścia, Vmax – prędkość maksymalna).
Opracowana metoda została nazwana Dynamiczną Analizą Wektorów, a implementacja jej zakończyła się pełnym sukcesem. Przy skomplikowanej ścieżce narzędzia liczącej kilkadziesiąt tysięcy wektorów o długości całkowitej ok. 20m, przy zadanej prędkości posuwu 100mm/s i przy włączonej Dynamicznej Analizie Wektorów czas pracy wyniósł niecałe 4 minuty, natomiast z wyłączoną analizą ok. 20min. Ta kolosalna różnica w czasie pracy maszyny pozwala na osiągnięcie znacznych korzyści przy wykonywaniu prac wykorzystujących skomplikowane ścieżki narzędzia takich jak obróbka form wtryskowych, tłoczników, wykrojników, modeli odlewniczych, matryc i innych narzędzi.